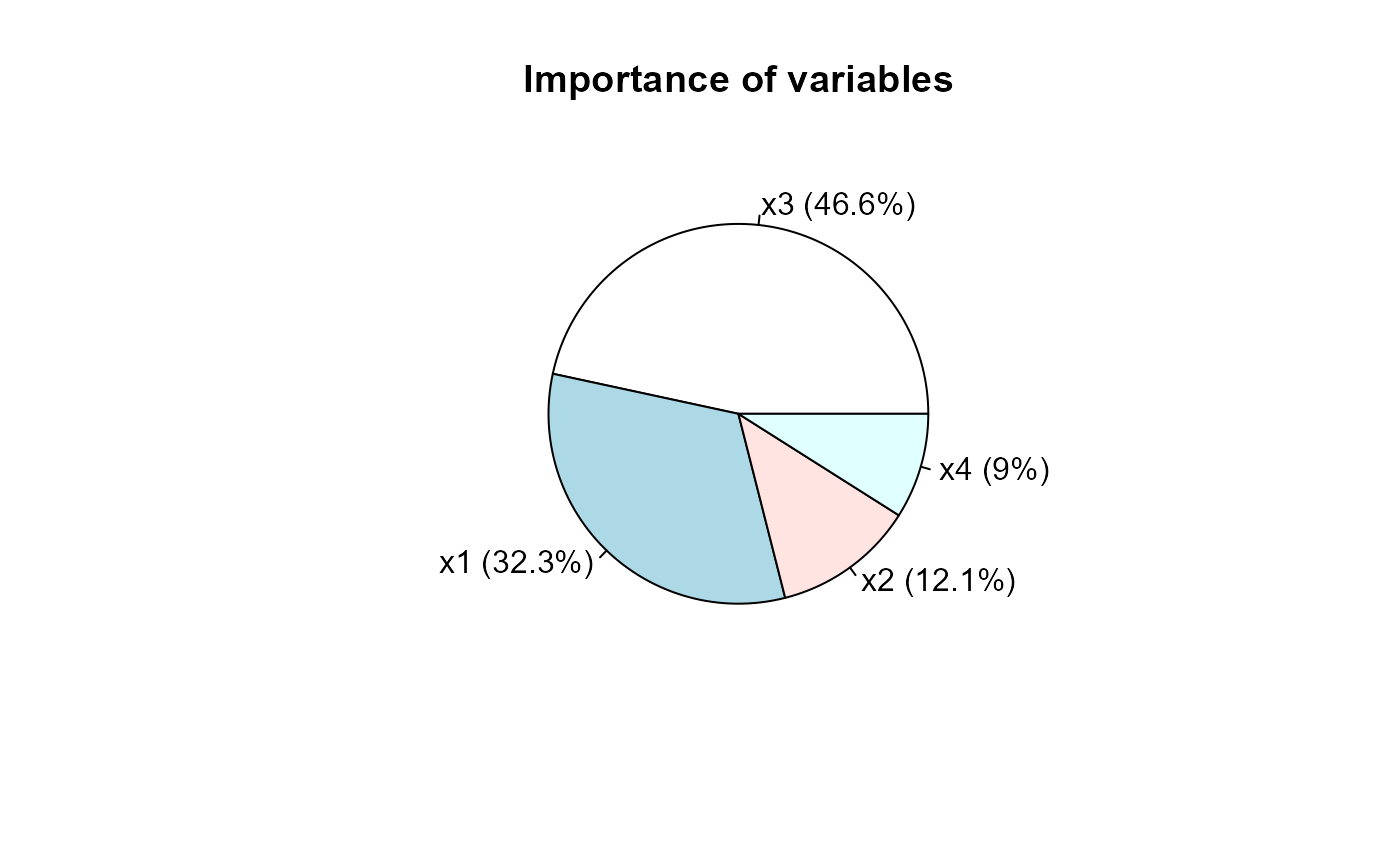
Importance of Variables According to the Singh (1981) Criterion

A function to calculate the Singh (1981) criterion for importance of variables based on the squared generalized Mahalanobis distance. $$S_{.j} = \sum_{i=1}^{n-1} \sum_{i'>i}^{n} (x_{ij} - x_{i'j}) * (\bold{x}_i - \bold{x}_{i'})' * \bold{\Sigma}_{j}^{-1} $$

# S3 method for default
singh(data, cov, inverted = FALSE)
# S3 method for singh
plot(x, ...)

Arguments

data	a data frame or matrix of data (n x p).
cov	a variance-covariance matrix (p x p).
inverted	logical. If FALSE (default), cov is supposed to be a variance-covariance matrix.
x	an object of class "singh".
...	further graphical arguments.

Value

singh returns a matrix containing the Singh statistic, the importance proportion and the cummulative proprtion of each variable (column) in data.

References

Singh, D. (1981) The relative importance of characters affecting genetic divergence. Indian Journal Genetics & Plant Breeding, 41:237-245.

Author

Anderson Rodrigo da Silva <anderson.agro@hotmail.com>

See also

D2.dist

Examples

# Manly (2004, p.65-66)
x1 <- c(131.37, 132.37, 134.47, 135.50, 136.17)
x2 <- c(133.60, 132.70, 133.80, 132.30, 130.33)
x3 <- c(99.17, 99.07, 96.03, 94.53, 93.50)
x4 <- c(50.53, 50.23, 50.57, 51.97, 51.37)
x <- cbind(x1, x2, x3, x4)
Cov <- matrix(c(21.112,0.038,0.078,2.01, 0.038,23.486,5.2,2.844,
  0.078,5.2,24.18,1.134, 2.01,2.844,1.134,10.154), 4, 4)
(s <- singh(x, Cov))
#>                              x3        x1        x2         x4
#> Singh statistic       5.4361584 3.7721798 1.4059118 1.04694241
#> Proportion            0.4661752 0.3234815 0.1205633 0.08978005
#> Cumulative proportion 0.4661752 0.7896567 0.9102200 1.00000000
#> attr(,"class")
#> [1] "singh"
plot(s)

# End (not run)